两点直线方程公式的推导与应用（探究直线方程公式的由来与应用范围）

在平面几何中，直线是最基本的几何概念之一。而对于直线的研究与描述，直线方程是一个非常重要的工具。本文将围绕直线方程公式展开，详细探讨其推导过程和应用范围。

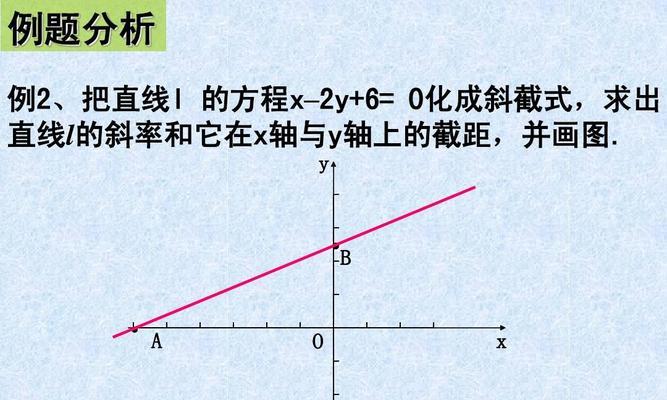
一、一点式方程的定义及推导

一、定义

二、推导过程

二、两点式方程的定义及推导

一、定义

二、推导过程

三、点斜式方程的定义及推导

一、定义

二、推导过程

四、斜截式方程的定义及推导

一、定义

二、推导过程

五、截距式方程的定义及推导

一、定义

二、推导过程

六、直线方程的应用范围与意义

一、在几何中的应用

二、在物理中的应用

三、在经济学中的应用

四、在计算机图形学中的应用

七、直线方程公式的优缺点分析

一、优点

二、缺点

八、常见问题解答

一、直线方程公式是否唯一？

二、如何根据已知条件选择最合适的直线方程公式？

三、直线方程公式的精确性如何保证？

九、直线方程公式的拓展与延伸

一、三维空间中直线方程的推导与应用

二、曲线方程与直线方程的联系与区别

十、实例分析：如何利用直线方程公式解决实际问题

一、问题描述

二、解题过程

三、实际应用

十一、直线方程公式的历史渊源与发展

一、直线方程公式的起源

二、发展历程

结尾

通过对直线方程公式的推导和应用的探讨，我们不仅加深了对这一基本概念的理解，还了解了直线方程的多样性和广泛的应用范围。直线方程公式在几何、物理、经济学和计算机图形学等领域都扮演着重要角色，为我们解决问题提供了有力的工具。掌握直线方程公式的原理和应用是我们在学习和实践中必不可少的一部分。

探秘两点直线方程公式的推导过程

在数学中，直线是最基本的几何图形之一，而求解直线方程是解决几何问题的重要一步。本文将详细介绍如何通过两点来推导直线的方程公式，并探讨这一公式的应用。

两点直线方程的基本概念

两点直线方程是指通过给定的两个坐标点来确定一条直线的方程，它能够提供关于直线的斜率和截距等重要信息，帮助我们更好地理解和分析直线。这个方程的形式通常是y=mx+b，其中m是斜率，b是截距。

斜率的计算方法

斜率是直线的重要特征之一，表示直线上每单位水平距离对应的垂直距离。斜率的计算方法可以通过两个给定点的坐标来求解，利用公式m=(y2-y1)/(x2-x1)，我们可以得到直线的斜率。

截距的定义与求解

截距是直线与y轴的交点，它可以通过两点直线方程求解得到。我们可以选择其中一个已知点代入方程，然后解出截距。截距的存在使得我们可以更方便地描绘直线在y轴上的位置。

两点直线方程公式的推导过程

推导两点直线方程的过程主要基于直线的斜率和截距。我们可以通过斜率和已知点的坐标得到斜截式方程，然后再根据已知点的坐标计算出截距，最终得到两点直线方程的标准形式y=mx+b。

两点直线方程公式的应用举例

通过两点直线方程公式，我们可以解决很多与直线相关的问题，例如求直线的交点、判断两条直线是否平行或垂直等。这个公式的应用广泛，是解决几何问题的重要工具。

两点直线方程与平行线的关系

当两条直线具有相同的斜率时，它们被称为平行线。利用两点直线方程的斜率可以帮助我们判断两条直线是否平行，进而解决与平行线相关的问题。

两点直线方程与垂直线的关系

当两条直线的斜率为互为倒数关系时，它们被称为垂直线。我们可以利用两点直线方程的斜率来判断两条直线是否垂直，进而解决与垂直线相关的问题。

两点直线方程与点斜式的转换

点斜式是直线方程的另一种形式，它利用已知点和斜率来表示直线的方程。通过两点直线方程公式，我们可以将其转换成点斜式，从而更灵活地应用于问题的求解。

两点直线方程的图形表示

两点直线方程可以通过图形来表示，通过绘制直线上的两个点，并利用斜率和截距的信息来确定整条直线。这样的图形表示可以帮助我们更好地理解直线的性质和特点。

两点直线方程与平面几何的关系

两点直线方程不仅在二维平面几何中有着重要应用，在三维空间中也同样适用。在三维几何中，我们可以通过两点来确定一条直线，并得到其方程。

两点直线方程在实际问题中的应用

两点直线方程在实际问题中也有广泛的应用，例如地图上两个城市之间的最短距离、机器人行走的轨迹规划等。通过两点直线方程，我们可以解决这些问题，并得到实际问题的具体答案。

两点直线方程的优缺点

两点直线方程作为解决直线问题的常用工具，具有简单明了、易于应用的优点。然而，当直线垂直于x轴时，斜率不存在，这个方程就无法使用，这是其主要的缺点之一。

两点直线方程的重要性和实用性

通过本文的介绍，我们可以看出两点直线方程在数学中的重要性和实用性。它是直线研究的基础，是解决几何问题的有效工具，也是其他数学领域中的基础知识。

两点直线方程公式的深入学习建议

对于想深入学习两点直线方程公式的读者来说，建议进一步探讨相关的数学概念，如点斜式、截距式等，并通过大量练习来提高运用方程公式解决问题的能力。

通过本文的介绍，我们详细了解了两点直线方程公式的推导过程以及其在解决直线问题中的应用。掌握这一公式将有助于我们更好地理解和分析直线，并且能够灵活地应用于实际问题的求解中。